[动态规划]动态规划入门

动态规划笔记之入门

何为动态规划？

（源自oi-wiki）动态规划是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。由于动态规划并不是某种具体的算法，而是一种解决特定问题的方法，因此它会出现在各式各样的数据结构中，与之相关的题目种类也更为繁杂。动态规划与递推类型可能有些类似。

动态规划的性质

1.无后效性

简单来说就是，处于某个状态的和过去发生过的任何事件没有任何关系，它的状态只会与未来的状态有关。也就是说过去的事件已经假定求解完成了，不会受到后续进行策略的任何影响。

2.子问题重叠

对于有大量子问题重叠的问题，可以开数组将之前的子问题答案存储起来，加快运行速度。

例如：求解斐波那契数列的第n项是多少？

1）暴力求解

#define int long long 
int fei(int x){
    if(x==1||x==0) return 1;
    return fei(x-1)+fei(x-2);
}

如果是这样求解的话，那么，他的运行模式就会变成下面这样：

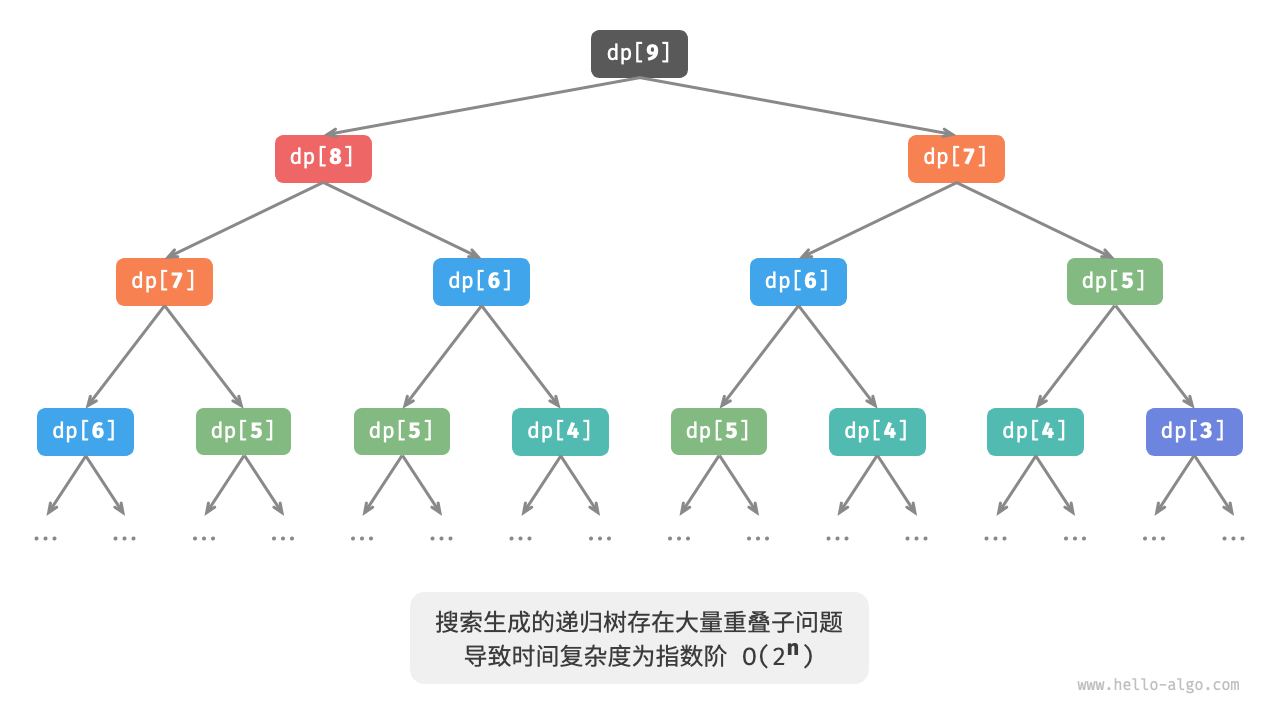
我们会发现这个会有很多的重复计算（时间复杂度是O(n^2))，这极大的影响了我们计算的时间复杂度。那重复计算的话，那我们不妨优化一下，如果说在递推求解的时候，如果之前已经访问或者说已经计算过了那么就直接跳过，那么，这就是我们接下来要说的记忆化搜索。

2）记忆化搜索

#define int long long 
const int N=2e5+10;
int vis[N];
int sum[N];
int fei(int x){
    if(x==1||x==0) return 1;
    if(vis[x]) return vis[x];
    return vis[x]=fei(x-1)+fei(x-2);
}

这个时候就会发现需要重复计算的数据就被sum数组存起来了，等到下一次用到的时候就可以直接使用了，时间复杂度大大减小了。可能说也算一种剪枝（？

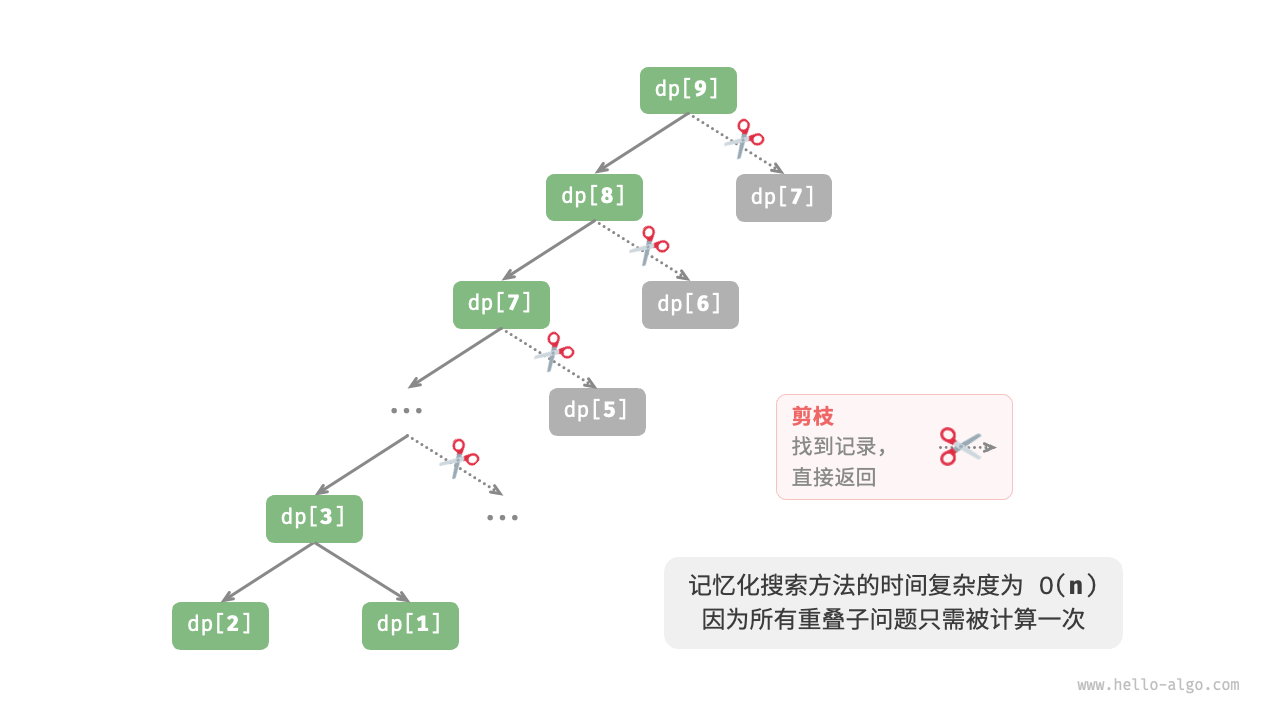
但是这样可能还是太费空间的怎么办？不想开两个数组记录。这个时候时候就需要使用动态规划了。

3）动态规划

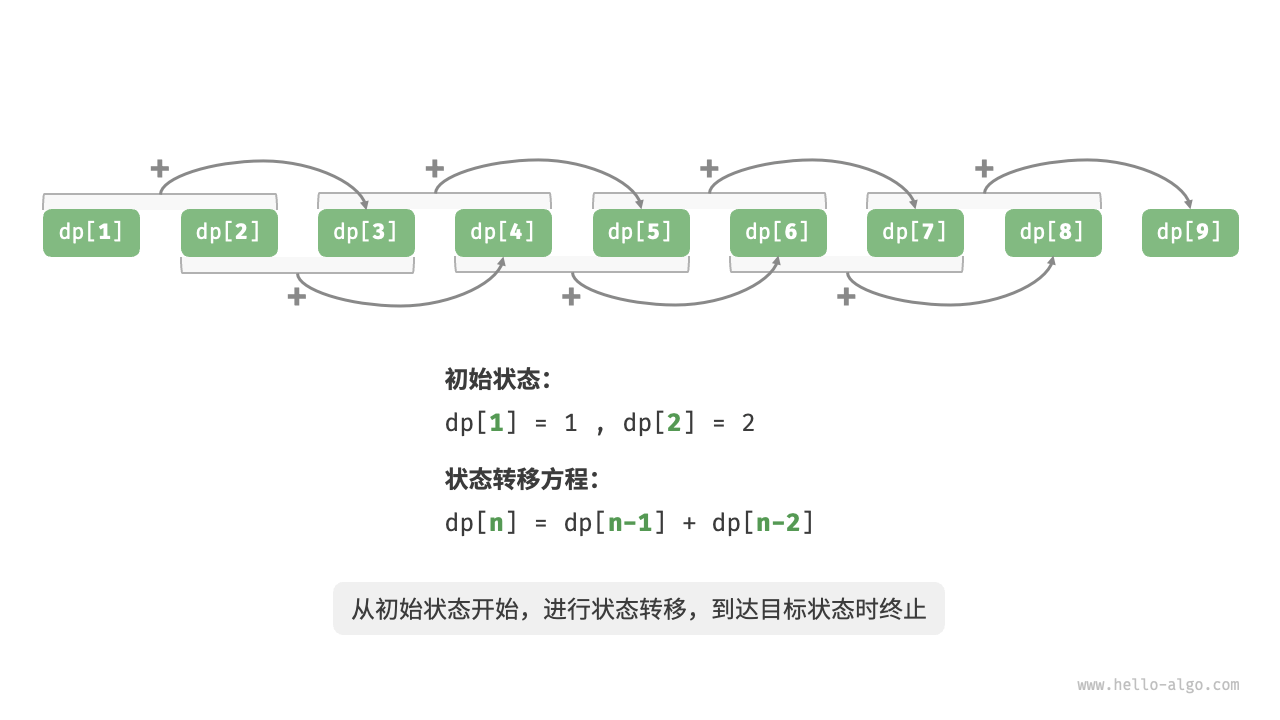
由于斐波那契数列的和是fei(1)=1,fei(0)=1,然后递推公式是fei(x)=fei(x-1)+fei(x-2);代码如下：

#define int long long
const int N=2e5+10;
int dp[N];
int main(){
    int n;cin>>n;
    dp[1]=1,dp[0]=1;
    for(int i=2;i<=n;i++){
        dp[i]=dp[i-1]+dp[i-2];
    }
    cout<<dp[n]<<endl;
}

上面所说的重叠子问题也就是把重复计算的过程，用空间提前储存好子问题的答案，等到需要用的时候，再快速拿出来使用，这样可以大大提高运行速率。如下：

3最优子结构

‌最优子结构‌是动态规划算法中的一个重要概念，它指的是一个问题可以分解为若干个子问题，且这些子问题的最优解能够组合成原问题的最优解。也就是对子问题进行最优计算，再合并成这个最大问题的最优解。

动态规划问题解题步骤

1.初始化数值

2.列状态转移方程

这里我们就写一个例题：

链接：https://ac.nowcoder.com/acm/problem/21302
来源：牛客网

题目描述

给你一个长度为50的数字串,问你有多少个子序列构成的数字可以被3整除
答案对1e9+7取模

输入描述:

输入一个字符串，由数字构成，长度小于等于50

输出描述:

输出一个整数

我们这里可以思考一下，数字串的话，可以化为只含0，1，2的string。

首先执行第一步：初始化，这一题没有特殊要求，直接全部赋值为0；

遍历一遍这个字符串，我们可以发现如下规律，如果该字符串的第i项为0的话，则第i项可以被3整除的数量是

$$dp[0][i]=dp[0][i-1]*2+1$$

如果第i项是1的话，第i项可以被3整除的数量更新成:

$$dp[0][i]=dp[0][i-1]+dp[2][i-1]$$

如果第i项是2的话，第i项可以被3整除的数量更新成:

$$dp[0][i]=dp[0][i-1]+dp[1][i-1]$$

然后每次计算完都要更新dp[1]与dp[2]的值，上边就是我们要找的状态转移方程。

代码如下：

void solve(){
    string s;
    cin>>s;
    for(int i=0;i<s.size();i++){
        a[i]=s[i]-'0';
    }
    int len=s.size();
    int m=(s[0]-'0')%3;
    dp[m][0]=1;
    for(int i=1;i<len;i++){
        m=(s[i]-'0')%3;
        if(m==0){
            dp[0][i]=(dp[0][i-1]*2+1)%mod;
            dp[1][i]=(dp[1][i-1]*2)%mod;
            dp[2][i]=(dp[2][i-1]*2)%mod;
        }
        if(m==1){
            dp[0][i]=(dp[0][i-1]+dp[2][i-1])%mod;
            dp[1][i]=(dp[1][i-1]+dp[0][i-1]+1)%mod;
            dp[2][i]=(dp[2][i-1]+dp[1][i-1])%mod;
        }
        if(m==2){
            dp[0][i]=(dp[0][i-1]+dp[1][i-1])%mod;
            dp[1][i]=(dp[1][i-1]+dp[2][i-1])%mod;
            dp[2][i]=(dp[2][i-1]+dp[0][i-1]+1)%mod;
        }
    }
    cout<<dp[0][len-1]<<endl;
}