对于已知一个数列(n项),你需要进行下面两种操作:
对于这个问题,如果使用前缀和或者暴力的话那么他的时间复杂度是O($n^2$),这很显然会TLE的。这个时候就需要使用树状数组这一数据结构来实现了,其时间复杂度是O($nlog(n)$).
接下来进入正题,介绍一下树状数组的实现。
顾名思义,树状数组就是很像树的数组。(确真)
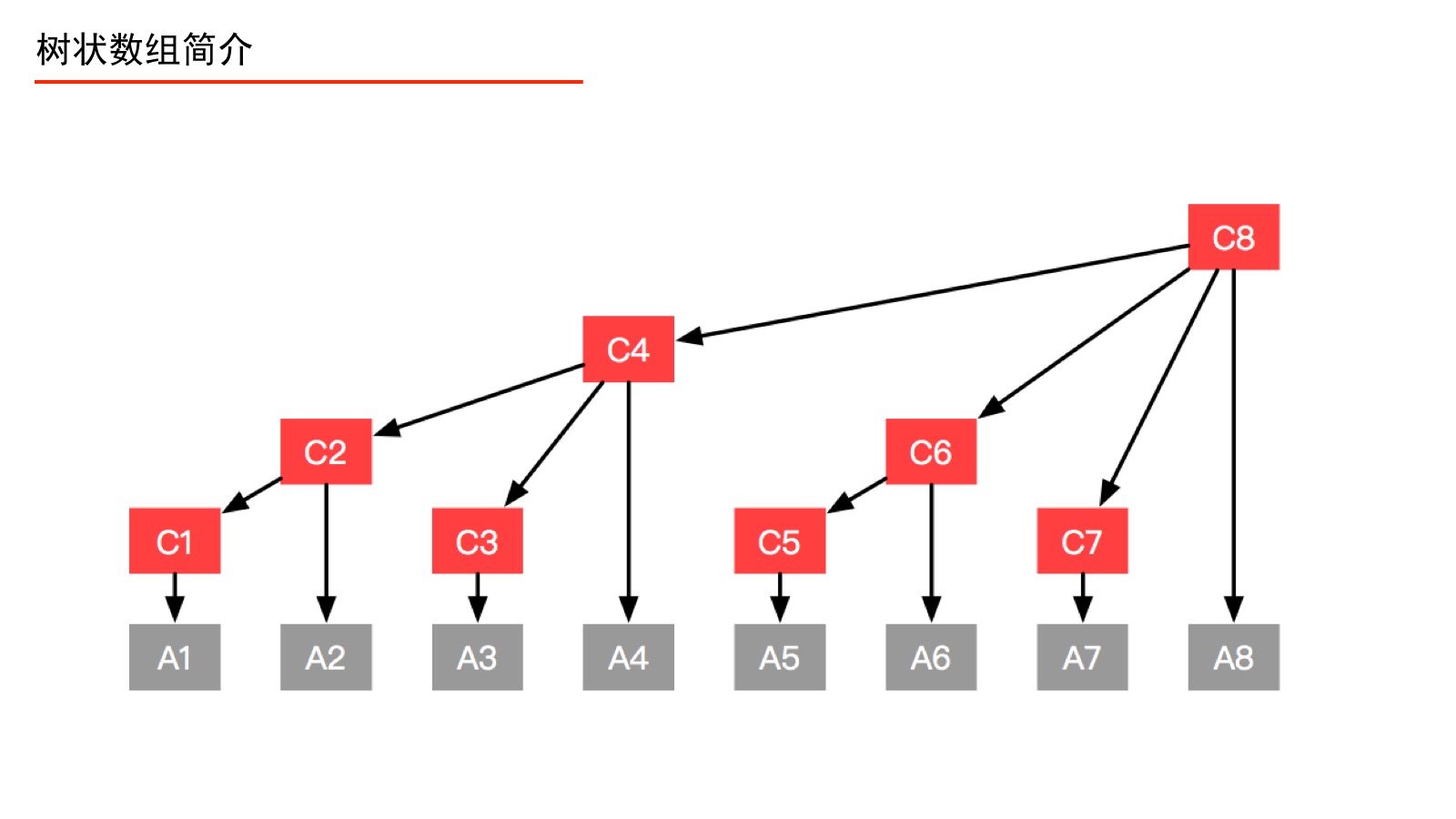
用二进制的思维方式看这个树状数组有如下规律:
c0001=a0001;c数组包含a数组的个数:1
c0010=a0010+a0001;c数组中包含a数组的个数:2
c0011=a0011;c数组中包含a数组的个数:1
c0100=a0001+a0010+a0011+a0100;c数组中包含a数组的个数:4
c5,c6,c7,c8也是同理的
从这里可以看出c数组中包含a数组中元素的个数由c数组下标的最低位1来确定。而且元素数目就是$2^k$(其中k就是最低位1的位数)。
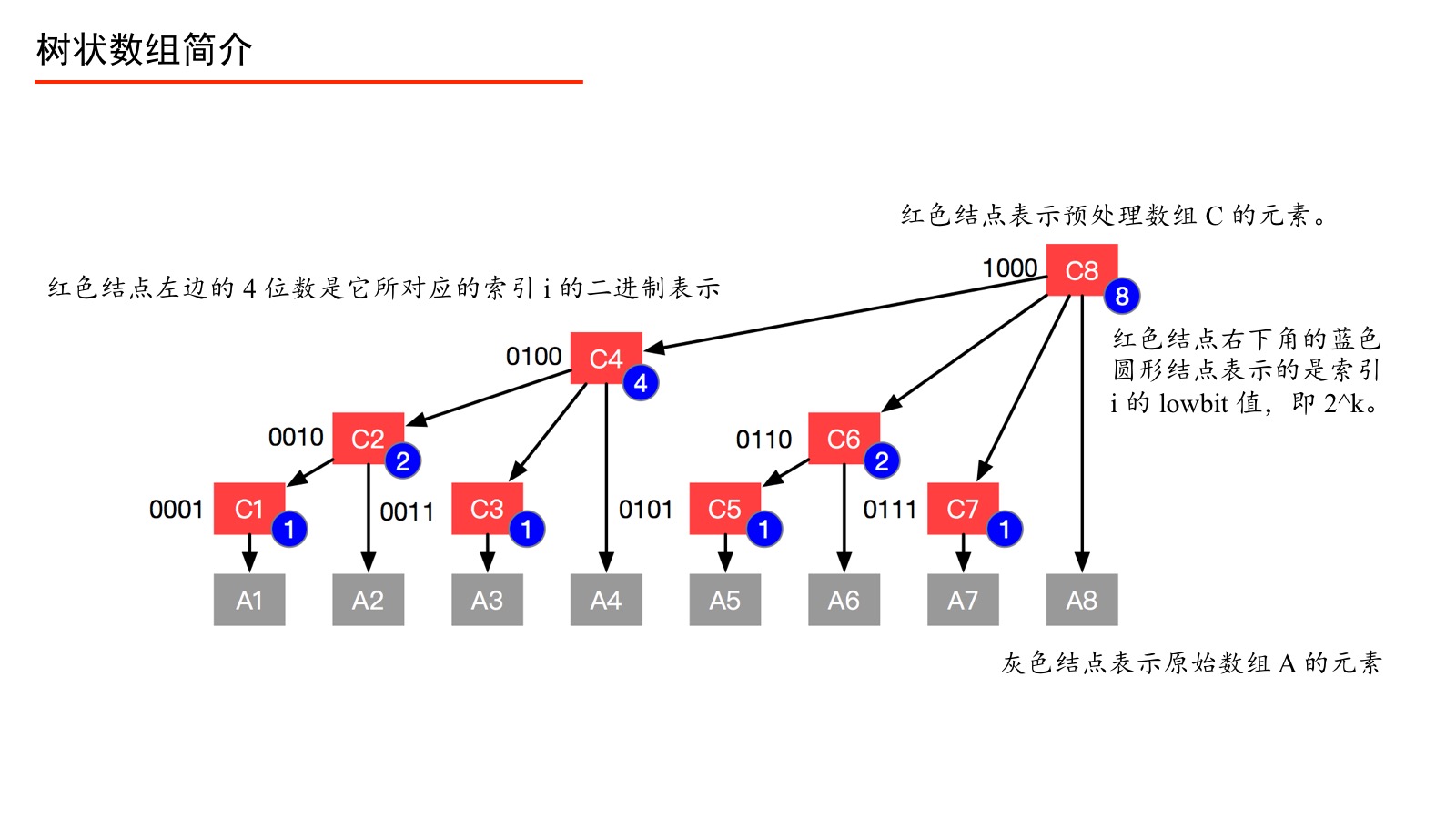
这里就要来介绍lowbit函数了!
lowbit函数用来快速计算二进制中最低位1出现的位置,下面来介绍一下原理:补码
比如:6的二进制就是0110,则其补码就是1001+1=1010,0110&1010=0010。
即c[6]中的元素个数就是$2^1$(0010);
所以我们定义一个lowbit函数来求c数组中当前下标对应a数组中元素的个数:
1
2
3
| int lowbit(int x){
return x&-x;
}
|
求完了个数之后就可以进行操作了;
对数组的预处理(add()函数):
1
2
3
4
5
6
| void add(int x,int y){
while(x<=n){
tree[x]+=y;
x+=lowbit(x);
}
}
|
求区间值ask()函数->对于一维数组来说:
1
2
3
4
5
6
7
8
| void ask(int x){
long long res=0;
while(x){
res+=tree[x];
x-=lowbit(x);
}
return res;
}
|
如下是树状数组可以实现的功能:
单点修改,单点查询:
1
2
| add(x,y);
ans=ask(x)-ask(x-1);
|
单点修改,区间查询:
1
2
| add(x,y);
ans=ask(r)-ask(l-1);
|
区间修改,单点查询:
这里使用差分的思想,创立一个b数组,来记录[l,r]中挂上+k标记的个数(即a数组每个元素+k的个数),维护树状数组。
1
2
3
| add(l,k);
add(r+1,-k);
ans=a[x]+ask(x);
|
区间修改,区间查询:
假设数组t1维护b[i]差分数组,数组t2维护i*b[i]前缀和。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| void add1(int x,int k){
while(x<=n){
t1[x]+=k;
x+=lowbit(x);
}
}
long long ask1(int x){
long long res=0;
while(x){
res+=t1[x];
x-=lowbit(x);
}
return res;
}
void add1(int x,int k){
while(x<=n){
t2[x]+=k;
x+=lowbit(x);
}
}
long long ask2(int x){
long long res=0;
while(x){
res+=t2[x];
x-=lowbit(x);
}
return res;
}
add1(l1,k);
add1(r1+1,-k);
add2(l1,(l1-1)*k);
add2(r1+1,-(r1*d));
ans=ask2(r1)*r1+ask(l1-1)-ask(r1)-ask(l1-1)*(l1-1);
|
以上是对于一维数组来说的。二维数组同理,主要差别就是差一层循环的事。
顺便粘贴一下HUT ACM组NO.1_Yue_chen学长的树状数组封装:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| template<class T>
struct BIT {
int n; vector<T> tr;
BIT() {}
BIT(int n) {init(n);}
void init(int n) {
this->n = n;
tr.assign(n+1, T());
}
void add(int x, T y=1) {
for(; x<=n; x+=(x&-x)) tr[x]+=y;
}
T query(int x, T y=0) {
for(; x; x-=(x&-x)) y+=tr[x];
return y;
}
T range(int l, int r) {
if(l == 0) return query(r);
return query(r) - query(l-1);
}
int kth(T k) {
int x = 0;
for (int i=1<<(int)log2(n); i; i/=2) {
if(x+i <= n and k >= tr[x+i-1]) {
x += i;
k -= tr[x - 1];
}
}
return x;
}
};
|

